SISTEM BILANGAN REAL
Sistem bilangan real berevolusi dari waktu ke waktu dengan memperluas gagasan tentang apa yang kami maksud dengan kata "angka." Pada awalnya, "angka" berarti sesuatu yang dapat Anda hitung, seperti berapa banyak domba yang dimiliki petani. Ini disebut bilangan asli , atau kadang-kadang bilangan penghitungan .
Bilangan Alami
atau “Menghitung Angka”
1, 2, 3, 4, 5,. . .
- Penggunaan tiga titik pada akhir daftar adalah notasi matematika umum untuk menunjukkan bahwa daftar terus berjalan selamanya.
Pada titik tertentu, gagasan "nol" mulai dianggap sebagai angka. Jika peternak tidak memiliki domba, maka jumlah domba yang dimiliki peternak adalah nol. Kami menyebut himpunan bilangan asli ditambah angka nol seluruh bilangan .
Seluruh Angka
Bilangan Alami bersama dengan "nol"
0, 1, 2, 3, 4, 5,. . .
Tentang Angka Nol
Apa itu nol? Apakah ini angka? Bagaimana jumlah yang tidak ada menjadi angka? Apakah tidak ada apa-apa, atau apakah itu sesuatu?
Nah, sebelum ini mulai terdengar seperti koan Zen, mari kita lihat bagaimana kita menggunakan angka "0." Sarjana Arab dan India adalah yang pertama menggunakan nol untuk mengembangkan sistem angka tempat-nilai yang kita gunakan saat ini. Ketika kita menulis angka, kita hanya menggunakan sepuluh angka 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Angka-angka ini dapat berdiri untuk angka, puluhan, ratusan, atau apa pun tergantung pada posisi mereka dalam angka. Agar ini berfungsi, kita harus memiliki cara untuk menandai tempat kosong dalam angka, atau nilai tempat tidak akan keluar dengan benar. Inilah yang angka “0” lakukan. Anggap saja sebagai wadah kosong, menandakan bahwa tempat itu kosong. Misalnya, angka 302 memiliki 3 ratusan, tanpa puluhan, dan 2 yang.
Jadi, apakah nol angka? Yah, itu masalah definisi, tetapi dalam matematika kita cenderung menyebutnya bebek jika bertindak seperti bebek, atau setidaknya jika perilakunya sebagian besar seperti bebek. Angka nol mematuhi sebagian besar aturan aritmatika yang sama dengan yang dilakukan angka biasa, jadi kami menyebutnya angka. Namun, ini adalah angka yang agak istimewa, karena ia tidak mematuhi semua hukum yang sama dengan angka lainnya — Anda tidak dapat membaginya dengan nol, misalnya.
Catatan untuk puritan matematika: Dalam pengembangan bidang aksiomatik ketat dari bilangan real, 0 dan 1 dipilih untuk perlakuan khusus. Nol adalah identitas aditif , karena menambahkan nol ke angka tidak mengubah angka. Demikian pula, 1 adalah identitas multiplikatif karena mengalikan angka dengan 1 tidak mengubahnya.
|
Yang lebih abstrak daripada nol adalah gagasan bilangan negatif. Jika, selain tidak memiliki domba, peternak berutang 3 domba, Anda dapat mengatakan bahwa jumlah domba yang dimiliki peternak adalah negatif 3. Butuh waktu lebih lama untuk menerima ide angka negatif, tetapi akhirnya mereka datang untuk dilihat sebagai sesuatu yang bisa kita sebut “angka.” Kumpulan angka diperluas yang kita dapatkan dengan memasukkan versi negatif dari angka penghitungan disebut bilangan bulat .
Integer
Seluruh angka plus negatif
. . . –4, –3, –2, –1, 0, 1, 2, 3, 4,. . .
Tentang Angka Negatif
Bagaimana Anda bisa memiliki kurang dari nol? Nah, apakah Anda memiliki akun giro? Memiliki kurang dari nol berarti Anda harus menambahkannya hanya untuk mendapatkannya hingga nol. Dan jika Anda mengambil lebih banyak dari itu, itu akan menjadi bahkan lebih jauh dari nol, yang berarti bahwa Anda harus menambahkan lebih banyak lagi hanya untuk mendapatkannya hingga nol.
Definisi matematis yang ketat berbunyi seperti ini:
Untuk setiap bilangan real n , ada kebalikannya , dilambangkan - n , sehingga jumlah n dan - n adalah nol, atau
n + (- n ) = 0
Perhatikan bahwa tanda negatif di depan angka adalah bagian dari simbol untuk angka itu: Simbol "–3" adalah satu objek — itu adalah singkatan dari "negatif tiga," nama nomor yang tiga unit kurang dari nol.
Angka nol adalah kebalikannya sendiri, dan nol dianggap bukan negatif atau positif.
Baca pembahasan pengurangan untuk lebih lanjut tentang arti dari simbol "-."
|
Generalisasi selanjutnya yang bisa kita buat adalah memasukkan ide fraksi. Meskipun kecil kemungkinannya bahwa peternak memiliki sejumlah kecil domba, banyak hal lain dalam kehidupan nyata yang diukur dalam fraksi, seperti setengah cangkir gula. Jika kita menambahkan pecahan ke himpunan bilangan bulat, kita mendapatkan himpunan bilangan rasional .
Angka rasional
Semua angka formulir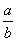 
, di mana a dan b adalah bilangan bulat (tetapi b tidak boleh nol)
, di mana a dan b adalah bilangan bulat (tetapi b tidak boleh nol)
Bilangan rasional mencakup apa yang biasa kita sebut pecahan
- Perhatikan bahwa kata "rasional" mengandung kata "rasio," yang seharusnya mengingatkan Anda pada pecahan.
Bagian bawah fraksi disebut penyebut . Anggap saja sebagai denominasi - ini memberi tahu Anda apa ukuran fraksi yang kita bicarakan: keempat, kelima, dll
Bagian atas fraksi disebut pembilang . Ini memberi tahu Anda berapa banyak perempat, perlima, atau apa pun.
- PEMBATASAN : Penyebut tidak boleh nol! (Tapi pembilangnya bisa)
Jika pembilangnya nol, maka seluruh fraksi sama dengan nol. Jika saya memiliki nol pertiga atau nol perempat, maka saya tidak punya apa-apa. Namun, tidak masuk akal sama sekali untuk berbicara tentang fraksi yang diukur dalam "nol".
- Pecahan dapat berupa angka yang lebih kecil dari 1, seperti 1/2 atau 3/4 (disebut pecahan yang tepat ) , atau pecahan bisa lebih besar dari 1 (disebut pecahan yang tidak tepat ) , seperti dua-dan-setengah, yang juga bisa kita tulis sebagai 5/2
Semua bilangan bulat juga dapat dianggap sebagai bilangan rasional, dengan penyebut 1:
Ini berarti bahwa semua set angka sebelumnya (bilangan asli, bilangan bulat, dan bilangan bulat) adalah himpunan bagian dari bilangan rasional.
Sekarang mungkin tampak seolah-olah himpunan bilangan rasional akan mencakup setiap kasus yang mungkin, tetapi tidak demikian halnya. Ada bilangan yang tidak dapat dinyatakan sebagai pecahan, dan bilangan ini disebut irasional karena tidak rasional.
Bilangan irasional
- Tidak dapat dinyatakan sebagai rasio bilangan bulat.
- Sebagai desimal, mereka tidak pernah mengulang atau mengakhiri (rasional selalu melakukan satu atau yang lain)
Contoh:
 |
Rasional (berakhir)
|
 |
Rasional (berulang)
|
 |
Rasional (berulang)
|
 |
Rasional (berulang)
|
 |
Tidak rasional (tidak pernah berulang atau berakhir)
|
 |
Tidak rasional (tidak pernah berulang atau berakhir)
|
Lebih lanjut tentang Bilangan Irasional
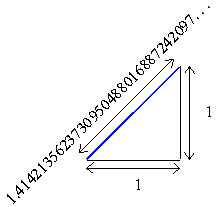
Mungkin terlihat bahwa bilangan rasional akan mencakup bilangan apa pun yang mungkin. Lagi pula, jika saya mengukur panjang dengan penggaris, itu akan keluar ke sebagian kecil - mungkin 2 dan 3/4 inci. Misalkan saya kemudian mengukurnya dengan lebih presisi. Saya akan mendapatkan sesuatu seperti 2 dan 5/8 inci, atau mungkin 2 dan 23/32 inci. Sepertinya betapapun dekat saya melihat itu akan menjadi sebagian kecil. Namun, ini tidak selalu terjadi.
Selamat! Anda baru saja menggambar panjang yang tidak dapat diukur dengan bilangan rasional apa pun. Menurut Teorema Pythagoras, panjang diagonal ini adalah akar kuadrat dari 2; yaitu, angka yang bila dikalikan dengan sendirinya memberi 2.
Menurut kalkulator saya,
Tetapi kalkulator saya hanya berhenti di sebelas tempat desimal karena tidak dapat menampung lagi. Angka ini benar-benar berlangsung selamanya melewati titik desimal, tanpa pola yang pernah berakhir atau berulang.
Ini karena jika polanya berhenti atau diulang, Anda dapat menulis angka sebagai pecahan — dan dapat dibuktikan bahwa akar kuadrat dari 2 tidak pernah dapat ditulis sebagai
untuk setiap pilihan bilangan bulat untuk a dan b . Bukti ini dianggap cukup mengejutkan ketika pertama kali ditunjukkan oleh pengikut Pythagoras 26 abad yang lalu.
|
Bilangan Nyata
- Rasional + Irasional
- Semua poin di garis angka
- Atau semua jarak yang memungkinkan pada garis bilangan
Ketika kita menempatkan bilangan irasional bersama dengan bilangan rasional, kita akhirnya memiliki set bilangan real yang lengkap. Angka apa pun yang mewakili jumlah sesuatu, seperti berat, volume, atau jarak antara dua titik, akan selalu berupa angka nyata. Diagram berikut ini mengilustrasikan hubungan set yang membentuk bilangan real.
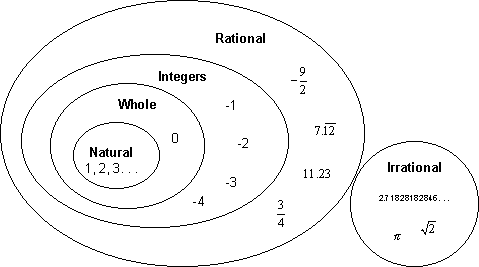
Set Dipesan
Bilangan real memiliki properti yang dipesan , yang berarti bahwa mengingat dua angka yang berbeda, kita selalu dapat mengatakan bahwa yang satu lebih besar atau lebih kecil daripada yang lain. Cara yang lebih formal untuk mengatakan ini adalah:
Untuk dua bilangan real a dan b , satu dan hanya satu dari tiga pernyataan berikut ini benar:
1. a kurang dari b , (dinyatakan sebagai a < b )
2. a sama dengan b , (dinyatakan sebagai a = b )
3. a lebih besar dari b , (dinyatakan sebagai a > b )
Garis Angka
Sifat urutan bilangan real memungkinkan kita mengaturnya di sepanjang garis (bayangkan bahwa garis tersebut terdiri dari jumlah titik tak terbatas yang semuanya saling berdekatan sehingga membentuk garis yang solid). Poin dipesan sehingga poin ke kanan lebih besar dari poin ke kiri:
- Setiap bilangan real sesuai dengan jarak pada garis bilangan, mulai dari pusat (nol).
- Angka negatif mewakili jarak ke kiri nol, dan angka positif adalah jarak ke kanan.
- Panah di ujung menunjukkan bahwa ia terus berlangsung selamanya di kedua arah.
Nilai mutlak
Ketika kita ingin berbicara tentang seberapa "besar" suatu angka tanpa memperhatikan apakah itu positif atau negatif, kita menggunakan fungsi nilai absolut . Nilai absolut dari angka adalah jarak dari angka tersebut ke titik asal (nol) pada garis angka. Jarak itu selalu diberikan sebagai angka non-negatif.
Pendeknya:
- Jika angka positif (atau nol), fungsi nilai absolut tidak melakukan apa pun untuk itu:
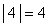
- Jika angka negatif, fungsi nilai absolut membuatnya positif:
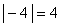
PERINGATAN : Jika ada aritmatika yang harus dilakukan di dalam tanda nilai absolut, Anda harus melakukannya sebelum mengambil nilai absolut — fungsi nilai absolut bekerja pada hasil apa pun yang ada di dalamnya. Misalnya, kesalahan umum adalah
(SALAH)
Hasil yang benar adalah
0 komentar:
Posting Komentar