FUNGSI & GRAFIK FUNGSI

Identifikasi Fungsi Menggunakan Grafik

HASIL PEMBELAJARAN

• Verifikasi suatu fungsi menggunakan tes garis vertikal
• Verifikasi fungsi satu-ke-satu dengan tes garis horizontal
• Identifikasi grafik fungsi toolkit

Seperti yang telah kita lihat dalam contoh di atas, kita dapat merepresentasikan fungsi menggunakan grafik. Grafik menampilkan banyak pasangan input-output dalam ruang kecil. Informasi visual yang mereka berikan sering membuat hubungan lebih mudah dipahami. Kami biasanya membuat grafik dengan nilai input di sepanjang sumbu horizontal dan nilai output di sepanjang sumbu vertikal.

Grafik yang paling umum menamai nilai inputdan nilai output , dan kita katakan y adalah fungsi dari x , atau y = f \ kiri (x \ kanan) ketika fungsi tersebut bernama f . Grafik fungsi adalah himpunan semua titik \ kiri (x, y \ kanan) dalam bidang yang memenuhi persamaan y = f \ kiri (x \ kanan) . Jika fungsi didefinisikan hanya untuk beberapa nilai input, maka grafik fungsi hanya beberapa titik, di mana x- koordinat dari setiap titik adalah nilai input dan y$x$$y$$y$$x$$y=f\left(x\right)$$f$$\left(x,y\right)$$y=f\left(x\right)$-Koordinasikan setiap titik adalah nilai output yang sesuai. Misalnya, titik-titik hitam pada grafik di grafik di bawah ini memberi tahu kami bahwa $f\left(0\right)=2$ dan $f\left(6\right)=1$ . Namun, himpunan semua poin $\left(x,y\right)$memuaskan $y=f\left(x\right)$ adalah kurva. Kurva yang ditampilkan termasuk $\left(0,2\right)$ dan $\left(6,1\right)$ karena kurva melewati titik-titik tersebut.

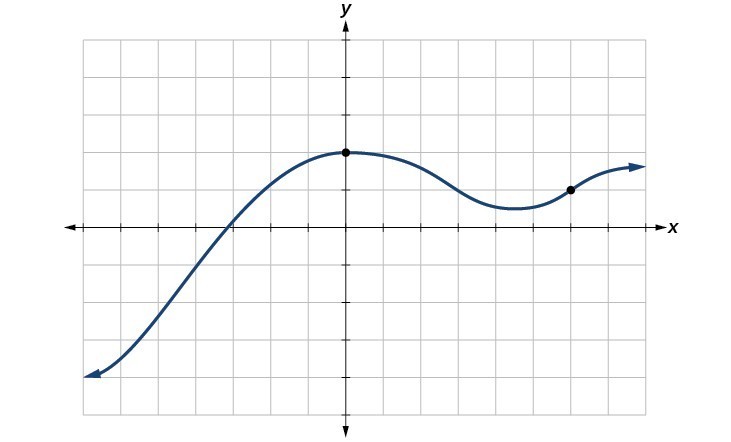
The uji garis vertikal dapat digunakan untuk menentukan apakah grafik mewakili fungsi. Garis vertikal mencakup semua titik dengan nilai tertentu . Nilai dari titik di mana garis vertikal memotong grafik merupakan output untuk nilai input tersebut . Jika kita dapat menarik setiap garis vertikal yang memotong grafik lebih dari sekali, maka grafik tidak tidakmendefinisikan suatu fungsi karena yang nilai memiliki lebih dari satu output. Suatu fungsi hanya memiliki satu nilai output untuk setiap nilai input.yxx$x$$y$$x$$x$

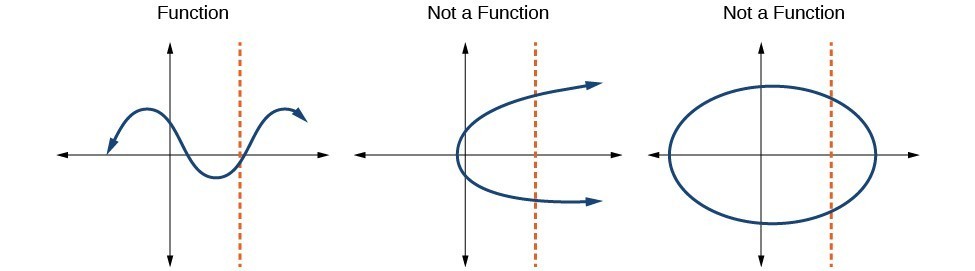
CARA: DIBERIKAN GRAFIK, GUNAKAN TES GARIS VERTIKAL UNTUK MENENTUKAN APAKAH GRAFIK MEWAKILI SUATU FUNGSI.

1. Periksa grafik untuk melihat apakah ada garis vertikal yang ditarik akan memotong kurva lebih dari satu kali.
2. Jika ada garis seperti itu, grafik tidak mewakili fungsi.
3. Jika tidak ada garis vertikal yang dapat memotong kurva lebih dari satu kali, grafik memang mewakili fungsi.

CONTOH: MENERAPKAN TES GARIS VERTIKAL

Manakah dari grafik yang mewakili fungsi$y=f\left(x\right)?$

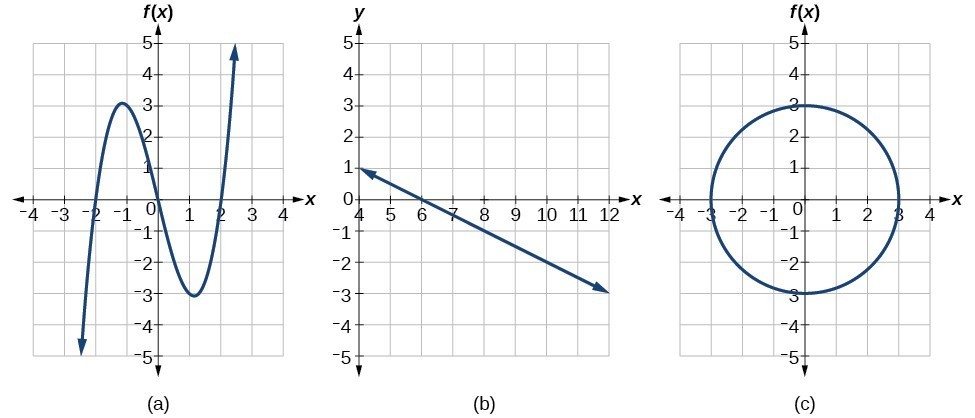
Tampilkan Solusi

COBALAH

Apakah grafik di bawah ini mewakili suatu fungsi?

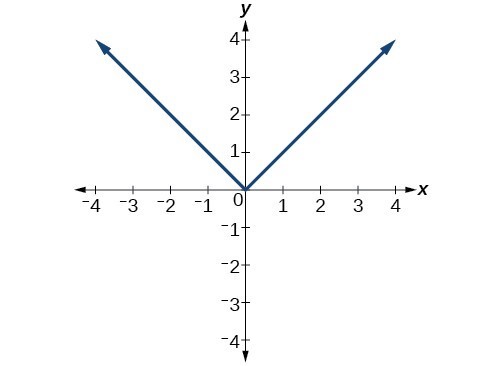
Tampilkan Solusi

Tes Garis Horisontal

Setelah kami menentukan bahwa grafik mendefinisikan fungsi, cara mudah untuk menentukan apakah itu fungsi satu-ke-satu adalah dengan menggunakan tes garis horizontal . Gambar garis horizontal melalui grafik. Garis horizontal mencakup semua titik dengan nilai tertentu . Nilai suatu titik di mana garis vertikal memotong suatu fungsi mewakili input untuk nilai keluaran itu . Jika kita dapat menarik setiap garis horizontal yang memotong grafik lebih dari sekali, maka grafik tidak tidakmewakili fungsi karena itu nilai memiliki lebih dari satu input.xyy$y$$x$$y$$y$

CARA: DIBERIKAN GRAFIK FUNGSI, GUNAKAN UJI GARIS HORIZONTAL UNTUK MENENTUKAN APAKAH GRAFIK MEWAKILI FUNGSI SATU-KE-SATU.

1. Periksa grafik untuk melihat apakah ada garis horizontal yang ditarik akan memotong kurva lebih dari satu kali.
2. Jika ada garis seperti itu, fungsinya bukan satu-ke-satu.
3. Jika tidak ada garis horizontal yang dapat memotong kurva lebih dari satu kali, fungsinya satu-ke-satu.

CONTOH: MENERAPKAN TES GARIS HORISONTAL

Pertimbangkan fungsi (a), dan (b) yang ditunjukkan dalam grafik di bawah ini.

Apakah salah satu dari fungsi satu-ke-satu?

Tampilkan Solusi

Mengidentifikasi Fungsi-fungsi Toolkit Dasar

Dalam teks ini kita mengeksplorasi fungsi — bentuk grafiknya, karakteristik uniknya, rumus aljabarnya, dan cara memecahkan masalah dengannya. Saat belajar membaca, kita mulai dengan alfabet. Ketika belajar melakukan aritmatika, kita mulai dengan angka. Ketika bekerja dengan fungsi-fungsi, itu sama membantu untuk memiliki satu set elemen dasar blok bangunan. Kami menyebutnya "fungsi toolkit" kami, yang membentuk serangkaian fungsi dasar bernama yang kami ketahui grafik, rumus, dan properti khusus. Beberapa fungsi ini diprogram untuk tombol individual pada banyak kalkulator. Untuk definisi ini kita akan menggunakan sebagai variabel input dan sebagai variabel output.y=f(x)$x$$y=f\left(x\right)$

Kita akan melihat fungsi toolkit ini, kombinasi fungsi toolkit, grafiknya, dan transformasi mereka di seluruh buku ini. Akan sangat membantu jika kita dapat mengenali fungsi-fungsi toolkit ini dan fitur-fiturnya dengan cepat berdasarkan nama, rumus, grafik, dan properti tabel dasar. Grafik dan nilai-nilai tabel sampel disertakan dengan masing-masing fungsi yang ditunjukkan di bawah ini.

Fungsi Toolkit
Nama	Fungsi	Grafik
Konstan	c$f\left(x\right)=c$ , di manaadalah konstanta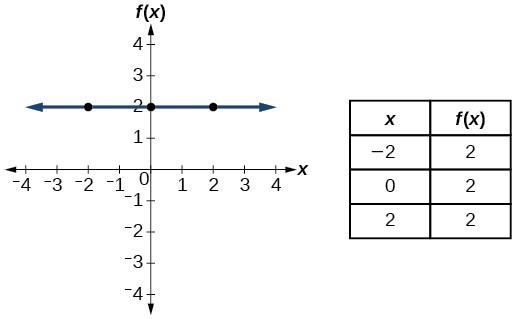$c$
Identitas	$f\left(x\right)=x$
Nilai mutlak	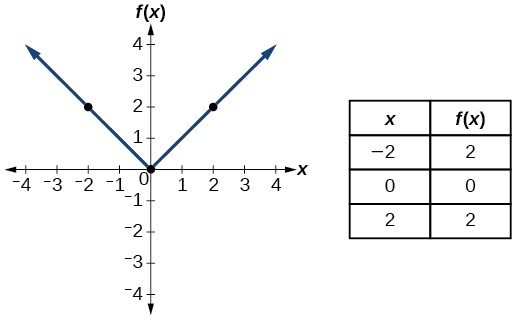$f\left(x\right)=|x|$
Kuadrat	$f\left(x\right)=x^2$
Kubik	$f\left(x\right)=x^3$
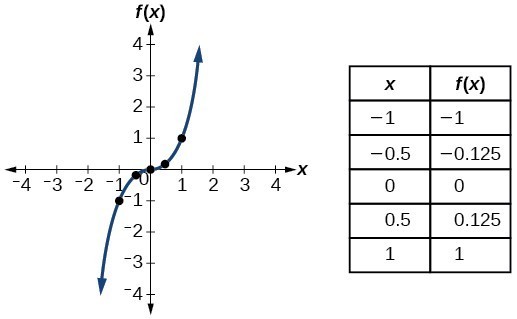Timbal Balik / Rasional	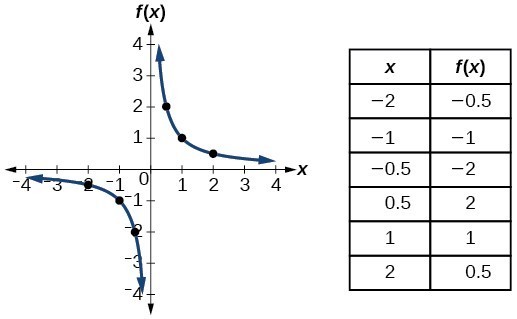$f\left(x\right)=\frac{1}{x}$
Timbal balik / Rasional kuadrat	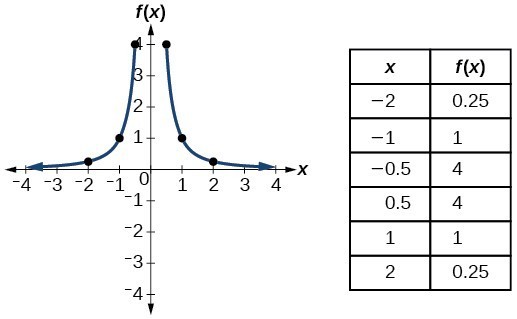$f\left(x\right)=\frac{1}{x^2}$
Akar pangkat dua	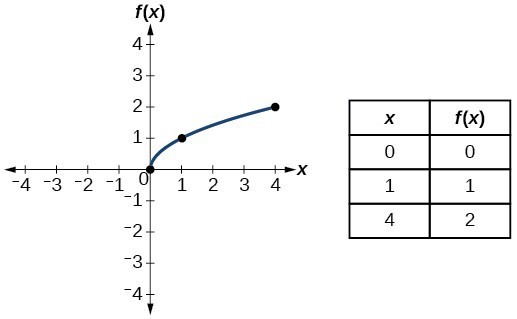$f\left(x\right)=\sqrt{x}$
akar pangkat tiga	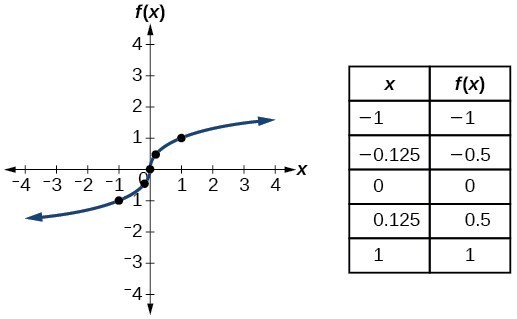$f\left(x\right)=\sqrt[3]{3x}$

COBALAH

COBALAH

Dalam latihan ini, Anda akan membuat grafik fungsi toolkit menggunakan alat grafik online.

1. Buat grafik setiap fungsi toolkit menggunakan notasi fungsi.
2. Buat tabel nilai yang merujuk fungsi dan setidaknya termasuk interval [-5,5].

Referensi : https://courses.lumenlearning.com/waymakercollegealgebra/chapter/identify-functions-using-graphs/

READMORE